So, before we go on with the details of what a coterminal angle calculator is or how to use it, let us take a quick recap of what coterminal angles are. Therefore, one defines coterminal angles as the angles that share the terminal side of an angle occupying the standard position. Hence, the next question must be what is the standard position? This means that one side of the angle is fixed along the positive x-axis. On the other hand, the vertex lies on the origin.
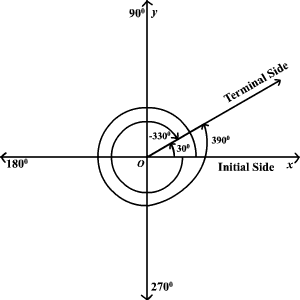
Therefore, if two angles are different but they have identical sides and vertices, they are coterminal angles. Moreover, you can also define them as angles that differ from each other by a whole number of complete circles. Therefore, all coterminal angles begin at the same side which is the initial side. On the other hand, they share the terminal side.
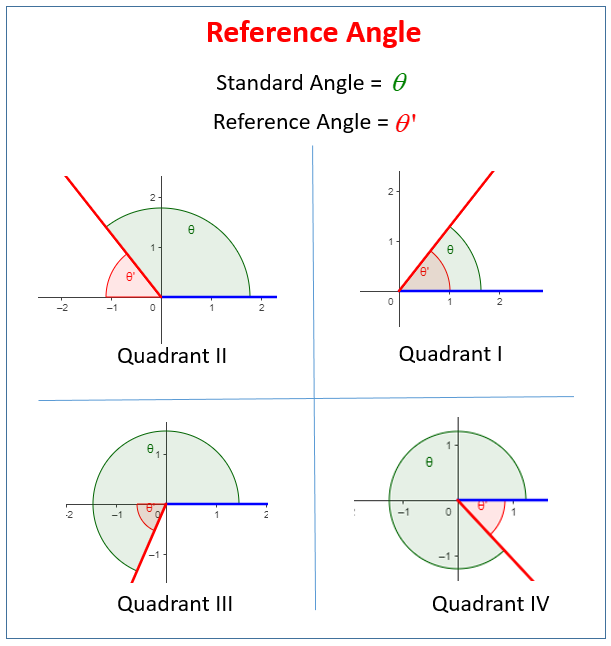
However, one thing might be often confusing. This is the difference that exists between the main reference angle with the definition of the coterminal angles. So, what you should keep in mind is that they are different things. The reference angle is the angle between the terminal side of the angle and the x-axis, and it’s always in the range of [0, 90] (or [0, π/2]).
Coterminal angle calculator formula
Finding coterminal angles might be confusing at times which is why you should need a coterminal angle calculator. However, blindly feeding in data to get the results is not a great idea. So, it is better to know the way the calculator works. This would reduce your own mistakes as well and you can verify the two answers.
So, if you want to find coterminal angles at a particular angle, you have to add or subtract a multiple of 360 degrees if you are working with degrees and 2pi if you are working with radians. Now, let us say the two angles are a and b. So, now you want to check whether they are coterminal. Hence, there are two formulas that the coterminal angle calculator uses as well. You need to verify the angles with either of them.
Formula to measure angles in degrees
b = a ± 360 * k, where k is a positive integer
Formula to measure angles in radians
b = a ± 2π * k, where k is a positive integer
Now, if you are well-versed with trigonometry, there is a feature that you can remember during verification of your coterminal angles. So, any two coterminal angles will have exactly the same trigonometric values. Now, what does this mean? Let us say a and b are coterminal angles. So, after we have found them out we can calculate their sines, cosines, or tangents. Therefore, all of these functions will have the exact same value for both. So, this is an easy way to understand if what you are doing is correct or not. Moreover, by this process, you can verify the result you have obtained via the coterminal angle calculator as well.
Coterminal angle calculator with steps
So, in the times of the internet, everything has become extremely easy. You cannot understand a math concept? Well, check online! So, calculating coterminal angles which used to be quite a confusing job has become really easy now! In case you are not bothered with the particular coterminal angle calculation, you can simply get the value from a coterminal angle calculator and use it for your bigger calculation. On the other hand, if you are just interested in its value, the coterminal angle calculator can act as a great verifier for results. At the end of the day, we all make mistakes while making calculations manually. Moreover, a little mistake here and there can mar all the efforts that we have spent in a long calculation.
There are many coterminal angle calculators available online. Here, let us take a look at the coterminal angle calculator from Omni Calculator to see how it works. Click on “Omni Calculator” and it will guide you to the link to the main calculator. So, you can do your calculations here as per the steps below.
Step 1 to use a coterminal angle calculator
So, at first, you go to the website and check the page. On the right-hand side, there is a detailed description of how to calculate coterminal angles. This will help you realize if you are making any mistakes while doing it manually. On the left top corner is the actual coterminal angle calculator. There are three boxes that you need to fill up if you want to get the right answer.
Step 2 to use a coterminal angle calculator
So, the first box says “I want to” and there are two options. So, you can either find the coterminal angles of a particular angle or see if two angles are coterminal. Therefore, click the correct option on the coterminal angle calculator as per your need. The next box says “angle in”. So, you might be doing the calculation in either degrees or radians. Therefore, the coterminal angle calculator can provide the value both ways. Select the correct option.
Step 3 to use a coterminal angle calculator
Now, if you want to find a coterminal angle as per a reference angle, there will be just one more box. It says “angle”. So, here you have to insert the reference angle whose coterminal angles you want to find. The coterminal angle calculator will instantly give you all the positive values. However, if you want to check if two angles are coterminal, then there will be two boxes. One box says “angle 1” and the other says “angle 2”. So, you enter the two angles in the coterminal angle calculator that you want to verify. If the two angles are coterminal, the coterminal angle calculator says, “ The two angles are coterminal”. If they are not, it says “The two angles are not coterminal.”
Step 4 to use a coterminal angle calculator
So, now the calculation is complete and you have got the result. Therefore, you can send the result as well. There is a “send this result” button just under the coterminal angle calculator. When you click it, it generates the link which you can share by copying. Or, you might also share it via Facebook, Twitter, LinkedIn, or e-mail.
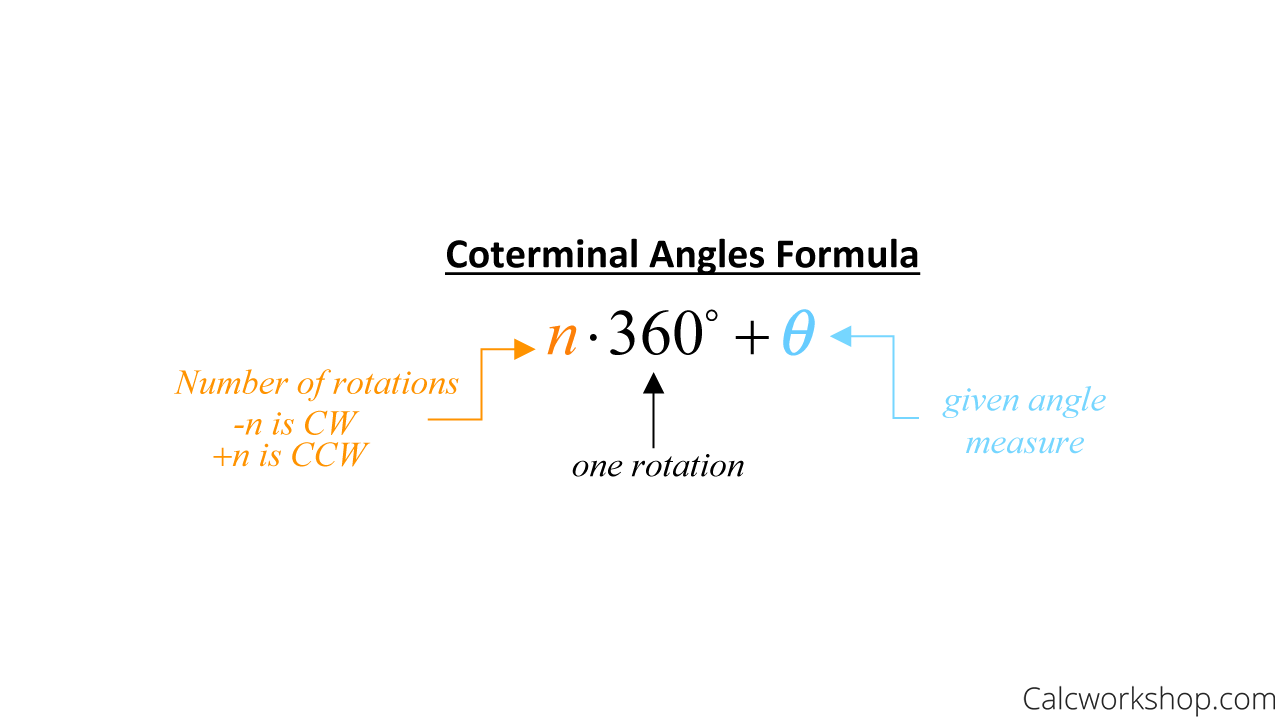
Coterminal angle calculator with radians
So, as we have already seen, you can find coterminal angles in both radians and degrees by using a coterminal angle calculator. Therefore, let us see at first how to get a result from a coterminal angle calculator in radians.
So, in the first step, select the option that says you want to find coterminal angles from a reference angle in the Omni calculator.
In the second step, click on the option that says “𝝿 radians”.
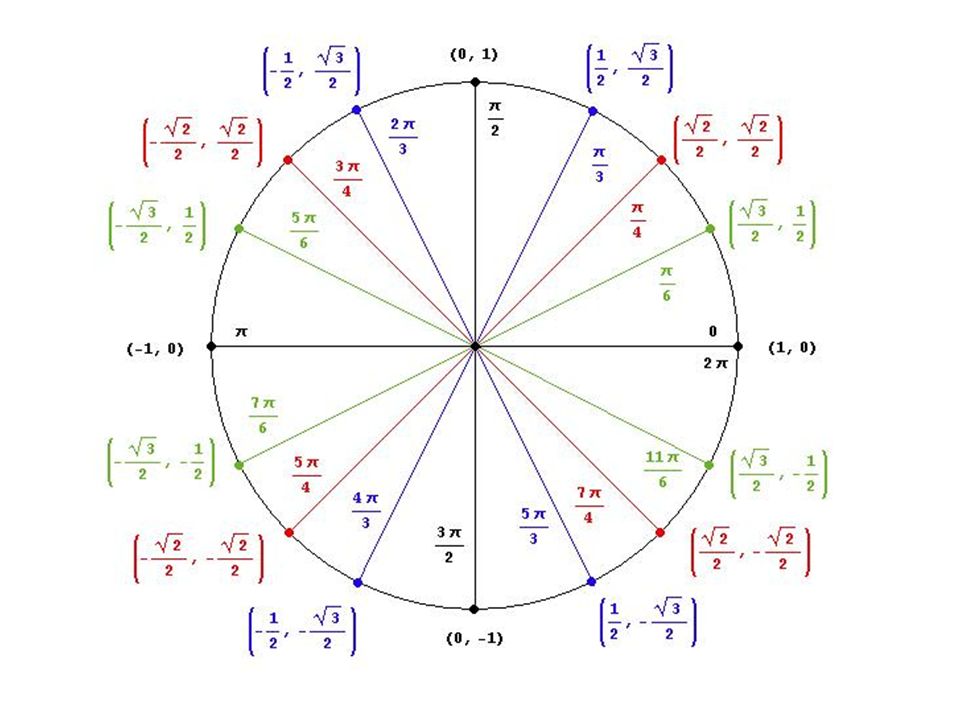
Therefore, now in the next box, you already have a 𝝿 symbol. You simply need to enter an integer. Let us say, you enter 3. Therefore, the angle that you are checking is 3 pi.
Now, it proves a rather elaborate answer. It converts the angle into degrees as well. So, in this case, it is 540 degrees. So, it has found a coterminal angle in [0, 2π) range: 1 π, located in the positive x-axis. Therefore, this angle has both positive and negative coterminal angles. The coterminal angle calculator finds both. So, in this case, there are four positive coterminal angles. They are 3 pi, 5 pi, 7 pi, and 9 pi. On the other hand, there are four negative coterminal angles as well. So, these are -1 pi, -3 pi, -5 pi, and -7 pi. (Remember, pi means 180 degrees)
Now, you might want to check whether two angles are coterminal as well. So, select the correct option. After this select the pi radians option. Now, there are two angles and the pi symbol is fixed. You have to enter two integers in both cases. Let us say, you enter 3 (as in 3 pi) in angle 1 and 5 (as in 5 pi) in angle 2. So, you get the result that the two are coterminal angles.
Coterminal angle calculator degrees
So, just how you can find or verify coterminal angles in radians, you can get them in degrees too from a coterminal angle calculator. Therefore, let us see how to do this with the help of an example.
So, in the first step, select the option that says you want to find coterminal angles from a reference angle in the Omni calculator.
In the second step, click on the option that says “degrees”.
Therefore, now in the following box, you already have a degrees symbol. So, enter the value of the reference angle of whose coterminal angles you want to find. Let us say, you enter 45, as in 45 degrees.
So, you get quite a detailed answer. At first, the coterminal angle calculator shows what the value will look like in radians. So then, the coterminal angle calculator will provide a list of both positive and negative coterminal angles that are possible. Now, in this case, the number of coterminal angles is really too many. So, the calculator provides a number of them but not all. The positive coterminal angles are 405°, 765°, 1125°, 1485° and so on. On the other hand, the negative coterminal angles are -315°, -675°, -1035°, -1395° and so on. There can be infinite ones.
Read Also: Calculating Formal Charge: Definition & Formula
However, if you are looking for a particular value, you can simply use the check whether two angles are coterminal parts. So, enter both the values in degrees. The calculator will tell you whether the angles are coterminal or not. Let us say, angle 1 is 45 degrees, and angle 2 is 90 degrees. Therefore, the two are not coterminal.

Coterminal angle calculator with pi
However, one thing is very important while you are checking if two angles are coterminal. Remember both the angles must be fed in the same unit into the coterminal angle calculator. Hence, if you are using degrees, you must use degrees for both cases. On the other hand, if you are using pi radians, make sure you are using pi for both cases. So, what this means is you cannot expect the calculator to recognize the difference in units. Moreover, it will not keep one intact, convert another and then compare. It can only compare when you have entered the data correctly.
Moreover, another very important part is you know the relationship between degrees and pi radians very well. So, to convert from radians to degrees, multiply the radians by 180°π radians. Therefore, what this means is pi denotes 180 degrees, both positive and negative. So, when you are saying ¼ pi, it means 45 degrees. Now, if you mess up the calculation and enter 45 radians instead of 45 degrees, the calculation will go haywire. This is because the value will now become 45 pi meaning 45 X 180 degrees which are 8100 degrees.
So, be very precautious with the units because students generally make mistakes here. When the unit changes, the meaning changes. Moreover, this is something that your coterminal angle calculator will not be able to detect. 8100 degrees is nothing absurd for a mechanical device. Therefore, it will simply evaluate and give you the answers that you need.

Coterminal angle calculator degrees minutes seconds
Now, you might not always represent angles in integers. So, you might have the value of an angle like x degrees, y minutes, z seconds. It is valid as an angle. However, this is not something that your coterminal angle calculator will accept. Therefore, you have to enter only integer values for getting coterminal angles. That is how the coterminal angle calculator works. However, you can enter an angle like 45.5 if you are checking it with another angle whose value also you will provide. But, in either case, there is no option to insert the value in terms of minutes or seconds. So, convert the minutes and seconds to degrees and feed in the final value to your coterminal angle calculator.

Coterminal angle calculator degrees with solution
So, let us check a few examples to clarify the concept.
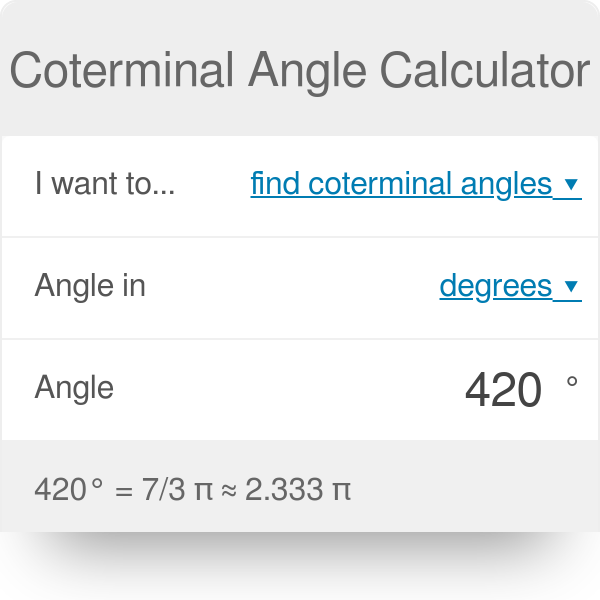
1. Let us say you want to find the coterminal angles of 60 degrees.
So, you enter the value after selecting the unit properly. Now let us see what answer your coterminal angle calculator provides.
60° = 1/3 π ≈ 0.333 π
Positive coterminal angles: 420°, 780°, 1140°, 1500°…
Negative coterminal angles: -300°, -660°, -1020°, -1380°…
So, there are many coterminal angles on both sides.
2. Let us say you want to check if 60 degrees and 120 degrees are coterminal.
So, you enter both values after selecting the unit properly. Therefore, 60 degrees mean pi/3 and 120 degrees mean pi/2. So, the calculator gives the answer that the two angles are not coterminal.
3. Let us say you want to find the coterminal angles of 270 degrees.
So, you enter the value after selecting the unit properly. Now let us see what answer your coterminal angle calculator provides.
270° = 3/2 π
Positive coterminal angles: 630°, 990°, 1350°, 1710°…
Negative coterminal angles: -90°, -450°, -810°, -1170°…
So, there are many coterminal angles on both sides.
Note: When we see the word “reference angle” while talking about the calculations specifically, it simply means the angle that you are entering. So, it might be negative too.
Coterminal angle calculator FAQs
How do you calculate coterminal angles?
Ans. So, if your reference angle is in degrees, add or subtract 360 degrees from it to find its coterminal angles. On the other hand, if your reference angle is in pi radians, add or subtract 2 pi from it to find its coterminal angles. Check the coterminal angle calculator formula part of the article to get a detailed discussion on how to calculate coterminal angles. Moreover, they can be both positive and negative.
How do you know if two angles are coterminal?
Ans. So, for this, you have the coterminal angle calculator. It will check if two angles are coterminal. The principle is that if two angles are drawn, they are coterminal if both their terminal sides are in the same place. So, what this means in simple words is that they lie on top of each other.
How do you find coterminal angles greater than 360 degrees?
Ans. So, if your angle has a value higher than 360 degrees, it is best to convert it into pi radians format. Therefore, enter the data into your coterminal angle calculator. So, it will give you the answer again in pi radians. This is because handling such big values with degrees might be very difficult.
Can an angle be coterminal with itself?
Ans. Yes, any angle is coterminal with itself.
How does radian measure an angle compared to the degree measure?
Ans. So, as we have already seen, 1 radian means 180 degrees. This is because an entire circle is 360 degrees or 2 pi radians. However, you use radians as a unit of measurement only when you are at least in high school because to understand it, you need a basic understanding of trigonometry.
What does the terminal side mean?
Ans. So, there is a standard definition for this. It is a straight line that has been rotated around a point on another line to form an angle measured in a clockwise or counterclockwise direction from the initial side.

Can the reference angle be negative?
Ans. No, the reference angle cannot be negative because it does not exist. It lies between 0 and pi/2 with very inclusive borders.
Are coterminal angles infinite?
Ans. Yes, quite so. Any angle might have infinitely many coterminal angles. This is because you can go on adding or subtracting 360 degrees. This is why your coterminal angle calculator mentions a few but not all of them. It is practically impossible to do so.
What is the smallest positive angle coterminal with?
Ans. It depends on the angle that you are dealing with. The smallest positive angle coterminal with any angle is to be found by adding or subtracting just one 2pi. So, if the angle is itself positive, but subtracting 2pi gives a negative value, it is the angle itself. On the other hand, if the angle is itself negative, we need to see the first positive angle after adding 2pi. So, it works that way.
What is the importance of a reference angle?
Ans. So, the reference angle is important for any trigonometric calculations. It is just a way to simplify the calculation of the values of trigonometric functions at various angles. If you are using a coterminal angle calculator, it is easy to calculate the value of any function at any angle.