The Double Integral Calculator is a free online tool that displays the double integral function’s value. However, we can calculate the value of a double integral using the Double Integral Calculator. One can also calculate the area of a two-dimensional figure using a double integral calculator. The symbol for double integration is ∫∫. However, we can use double integrals to calculate the volume beneath a surface. However,we can also calculate the average value of a two-variable function. Next, fill in the values in the input boxes to use the Double Integral Calculator.
Double Integral Calculator With Steps
Meanwhile, to use the online double integral calculator one must follow the instructions given below:
Step 1:
Use our Double Integral Calculator online.
Step 2:
In the provided input fields of the double integral calculator, enter the function as well as the restrictions. Then choose which variable you want to integrate first from the drop-down selection.
Step 3:
Then, to obtain the value of the double integral, click the “Calculate” button of the double integral calculator.
Step 4:
However, to clear the fields and input new values, click the “Reset” option.
How Does Double Integral Calculator Work?
Lets see how a Double integral calculator works. However, simple integration, double integration, and triple integration are all types of integrations that we can see in integral calculus. When dealing with a function in a single variable, the integration is done over a while (one-dimensional space). As a result, when we have a function that is dependent on two variables, we integrate it over an area.
However, if we have a double integral denoted by ∫∫ f (x, y) dx dy, we may find its value using the procedures below.
Try to solve the inner integral first. We shall first integrate the function concerning x because dx occurs before dy. However, one can treat all terms that include the letter y as constants.
However, as we already used the definite integral’s inner limits, our function will now only be defined in terms of y.
Meanwhile, apply the limits of the outer integral to get the final value.
As a note, the integral value of ∫dc∫da f(x, y) dx dy will be equal to ∫ba∫dc f(x, y) dy dx.
Double Integrals Definition
In short, the integral of a nonnegative function equals the area under the graph, as we learned in one-variable calculus. However, the volume of the region under the graph of a non-negative function f(x, y) defined on a region in the plane is associated with the double integral of f(x, y) (x, y). Meanwhile, double integrals are a two-dimensional integration method. Above all, they allow us to compute the volume beneath a surface, among other things.
Multiple integral is a definite integral of a function of several real variables in mathematics (particularly multivariable calculus), such as f(x, y) or f(x, y, z). Double integrals are integrals of a function of two variables over an area in R² (the real-number plane), whereas triple integrals are integrals of three variables over a region in R³ (real-number 3D space). However, see the Cauchy formula for repeated integration for numerous integrals of a single-variable function.
Double Integrals Calculator Theorem
Theorem: If f(x, y) is continuous on the rectangle Q = [a, b] × [c, d], then f is integrable on Q.
Fubini’s Theorem:
However, we utilize the second FTC to calculate integrals in the one-variable scenario. Fubini’s theorem is a method for calculating double integrals based on the following result. In essence, it divides a double integral into two one-dimensional integrations.
Meanwhile, the function defines the volume of the region between the surface (on the three-dimensional Cartesian plane where z = f(x, y)). Similarly, the double integral represents the plane that contains its domain of a positive function of two variables. In short, it is just as the definite integral of a positive function of one variable represents the area of the region between the graph of the function and the x-axis. A multiple integral produces hypervolumes of multidimensional functions when there are more variables.
Read Also:Distributive Property Calculator: Formula, steps, examples and more
However, the most typical representation of multiple integrations of a function in n variables, f(x1, x2,…, xn) over a domain D is nested integral signs in reverse order of execution, followed by the function and integrand arguments in an appropriate order. For each argument over each integral sign, a variable at the rightmost integral sign either symbolically expresses or abbreviates the domain of integration.
The conventional definition of the indefinite integral does not instantly extend to the multiple integral since the concept of an antiderivative is only specified for functions with a single real variable.
Double Integrals Calculator Formula
Moreover, we can call a double integral to be an integral of a two-variable function f (x, y) over a region R. Iterated integration can be used to solve the double integral if R = [a, b] × [c, d] (integrate first concerning y, and then integrate concerning x).
Double Integral (x^2+y^2)dxdy
convert it to polar rdrd0. and then solve. the circle is at (1,0) not the origin.
x² + y²=2x
(x-1)² + y²=1
Then x = 1+ rcosθ, y = rsinθ; dxdy = rdrdθ and x² + y² = (1+ rcosθ)² +sin²θ = 1+ r² + 2rcosθ.
D= {(r, θ): 0≤r≤1, 0≤θ≤2π}
Then
∫∫D(x² + y²)dxdy=∫∫D(r + r³ +2r²cosθ) drdθ = 3π / 2
Double Integral Calculator Properties
Many features of multiple integrals are similar to those of single-variable integrals (linearity, commutativity, monotonicity, and so on). Under certain situations, the value of multiple integrals is independent of the order of integrands, which is an important property of multiple integrals. Fubini’s theorem is the name given to this property.
Double Integral Examples
Example 1
Find the volume V under the plane z=8x+6y over the rectangle R=[0,1]×[0,2].
Ans. What we see is
f(x,y)=8x+6y≥0 for 0≤x≤1 and 0≤y≤2
so:
V=∫20∫10(8x+6y)dx dy
=∫20(4x² + 6xy ∣∣ x=1, x=0)dy
=∫20(4 + 6y)dy
=4y+3y² ∣∣20
=20
Assume that the integration order had been reversed. We can confirm that we’re still getting the same result:
V=∫1,0∫2,0 (8x + 6y)dy dx
=∫1,0(8 xy + 3y² ∣∣ y=2, y=0)dx
=∫1,0(16x + 12)dx
=8x²+12x∣∣10
=20
Example 2
Find the volume V under the surface z=e^(x+y) over the rectangle R=[2,3]×[1,2].
Ans. We know that
f(x,y)=ex+y>0 for all (x,y)
so,
V=∫2,1∫3,2 (ex+y) dxdy
=∫2,1(ex+y ∣∣x=3,x=2)dy
=∫2,1{e^(y +3) − e^(y +2)}dy
=e^(y + 3) − e^(y + 2 ) ||2,1
=e^5 −e⁴ −(e⁴ − e³)
=e^5 −2e⁴ +e³
Example 3
Evaluate ∫2π0∫π0sin(x+y)dxdy
Ans.
We can see that f(x,y)=sin(x+y) is both + and – over the rectangle [0,π]×[0,2π]. So we still can evaluate the double integral:
∫2π,0∫π,0 sin(x+y)dx dy
=∫2π,0(−cos(x+y)∣∣x=π,x=0)dy
=∫2π,0(−cos (y+π) +cos y)dy
=−sin(y+π) + siny ∣∣2π,0
=−sin3π + sin2π − (−sinπ + sin0)
=0
Double Integral (x+y)dxdy
Here we know x= 0, y= 0, and y= 2-x, x= 2-y
So,
∫2,0 ∫(2-y),0 ( x + y)dx dy
= ∫2,0 | (x²/2) + xy | (2-y), 0 dy
Or, ∫2,0 [ { (2-y)² / 2} + y(2 – y) ] dy
=∫2,0 [ { ( 4 – 4y + y² )/ 2} + 2y – y² ] dy
=∫2,0 [ { (4 – 4y + y² )/ 2} + { (4y -2y²)/ 2} ] dy
Or, ∫2,0 [ (4 – y²) / 2 ] dy
=∫2,0 [ 2 – ( y² / 2) ]
=|2y – ( y³ / 6) | 2,0
Or, 4- 8/6
= 12/3 – 4/3
= 8/3
Double integral Calculator over a region, Rectangle
Assume we want to integrate a multivariable function f throughout an area A:
A= {(x,y)∈R²: 11 ≤ x ≤14; 7 ≤ y ≤ 10 } and f(x,y) = x² + 4y}
From this, we formulate the iterated integral
∫¹⁰₇∫¹⁴₁₁ ( x²+4y) dx dy
We do the inner integral first, concerning x and treating y as a constant because it is not an integration variable. The integral’s result, a function that depends only on y, is then integrated concerning y.
Then we integrated the result concerning y.
The order of integration is interchangeable in circumstances when the double integral of the absolute value of the function is finite, that is, integrating concerning x first and integrating concerning y first provide the same result. Fubini’s theorem states this. For example, reversing the sequence of the previous computation yields the same result:
Double integral Calculator over a normal domain
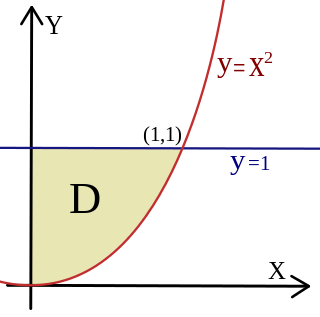
Consider the following region (as shown in the example graphic):
D= { (x,y) ∈ R²: x ≥ 0, y ≤ 1, y ≥ x²}
Calculate
∫∫D (x + y ) dx dy.
In terms of both the x- and y-axes, this domain is normal. To use the equations, you must first figure out what functions determine D and what intervals these functions are defined across. The two functions in this example are: ᵅ(x) = x² and ß(x) = 1
The interval is [a, b] = [0, 1] because the intersections of the functions with x = 0 determine the interval. (For a better visual understanding, we choose normality concerning the x-axis.)
It is now feasible to use the following formula:
(At initially, we compute the second integral with x set to a constant.) The remaining operations consist of applying basic integration techniques:
We could compute and achieve the same value if we choose normalcy concerning the y-axis.
Calculating Volume using Double integral Calculator
It is feasible to compute the volumes of some common solids using the methods discussed earlier.
Cylinder: The volume of a cylinder with a height of h and a circular base of radius R can be computed using polar coordinates by integrating the constant function h over the circular base. The formula for the volume of a prism agrees with this.
VOLUME = BASE AREA × HEIGHT
Sphere: Using spherical coordinates, one can calculate the volume of a sphere with radius R by integrating the constant function 1 over the sphere.
Tetrahedron: By integrating the constant function 1 over the tetrahedron with its apex at the origin and edges of length l along the x-, y-, and z-axes, the volume of a tetrahedron with its apex at the origin and edges of length l along the x-, y-, and z-axes may be computed.
This agrees with the formula for calculating the volume of a pyramid.
VOLUME = ⅓ × BASE AREA × HEIGHT = ⅓ × l²/2 × l = l³/6
Double Integral Calculator Application
The notion of a double integral calculator is used in a variety of sectors of science and engineering, including calculating the area of a two-dimensional region.
- Choosing the right loudness
- a large number of 2D plates
- On a two-dimensional plate, force
- The average of a function
- The moment of inertia and the centre of mass
- Dimensions of the surface
Some frequently asked questions about Double Integral Calculator
What is a double integral?
A line integral evaluates the function to be integrated along a curve, whereas a surface integral is a generalization of many integrals to integration over surfaces. It can be thought of as the line integral’s double integral analogue.
What are the differences between double and triple integrals?
When integrating over a two-dimensional region, we use a double integral. Similarly, when integrating over a three-dimensional region, we use a triple integral.
What does the second integral stand for?
The first integral produces the velocity v(t), and the second integral gives the displacement s if a(t) is the acceleration at time t. (t). That is likely the most important, if not the only, application of integrating twice that you will encounter this semester.
Can the total value of a double integral be zero?
That double integral instructs you to add all of the x²-y² function values over the unit circle. If you obtain a 0 here, that means the function either doesn’t exist in that region or it’s symmetrical over it.
What are the differences between integral and double integral?
We know Integrals over planar regions as double integrals. Integrals over curves, often known as the line or route integrals.
What does a double integral Calculator give?
If f(x,y)=1, the area of region R is given by the double integrals. The volume under the surface z=f(x,y) above the region R is equal to the integral. When R is a plate and f(x,y) is the density per unit area of the plate, the integral equals the plate’s mass.
How do you find the double integral area?
If we limit the region to the left by x = h¹(y) and on the right by h²(y) with c y d. We can also calculate the area using the double integral of 1 dxdy. Calculate the area between y = x² and y = x³ using the double integral.
How to Use the Double Integral Calculator?
Step 1:
In the input field, type the function and its bounds.
Step 2:
To receive the value, click the “Calculate” button.
Step 3:
Finally, in the new window, the result of the double integral will be revealed.
What is the use of a double integral Calculator?
The area of a region, the volume under a surface, and the average value of a function of two variables over a rectangular region are all calculated using double integrals.
Can you split up double integrals?
Fubini’s theorem, moreover, expresses the notion that double integrals can be broken into iterated integrals. Consider this theorem to be a necessary tool for calculating double integrals.
Does double integral order matter?
Although the order of integration is immaterial, we should use it to determine the integrals’ bounds.
What does triple integral represent?
A summation is a hypothetical fourth dimension represented by a triple integral.









