Completing the square method has the most common application in solving quadratic equations. In reality, it is one of the most used ways for solving the same problem.
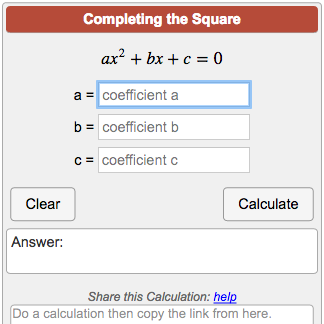
Completing the square Calculator:
Completing the square calculator is a free online tool that is quite simple to use.
It has several advantages:
- Very accurate results.
- Pretty easily available.
- Not at all time consuming, as compared to the pen-and-paper-based method.
- We do not need to know the mathematical formula for the ‘completing the square’ method.
Solve by completing the square calculator with steps
Initially, consider a quadratic equation of the form: ax^(2)+bx+c.
Step-1: Plug in the values of the quadratic coefficient(a), the linear coefficient(b) and, the constant or
free-term(c).
Step-2: Click on the ‘Calculate’ button.
The output box displays the value of the variable x accordingly.
Clearly, it is a hassle-free way of solving quadratic equations in a fraction of a few seconds.
The completing the square calculator is very easily available online or you can also use the one provided below:
Completing the square calculator vertex form:
In this method, the form of the given equation is changed such that the left side of the equation should be a perfect square binomial.
Actually, the Completing the square method is used for converting a quadratic equation of the form:
ax^(2)+bx+c=0
as a vertex of the form:
a(x-h)^2+k.
It can be done by rearranging the expression obtained after completing the square:
a*(x + m)2 + n, such that the left side is a perfect square trinomial.
Now, you can simply put this form of equation in the Completing the Square calculator.
Solve by Completing the square formula:
Completing the square method is a simple way to solve quadratic equations.
In reality, in case of a few equations of the form ax^{2}+bx+c=0, applying the factorization method of solving becomes a bit complicated.
For example,
If an equation is written as x^(2)+7x+3,
Clearly, we cannot find two numbers whose sum is 7 and whose product is 3. Thus, using the factorization method cannot solve this equation.
This means that we have to use an alternative way to get this done. This is where the Completing the square method comes into play.
Alternatively, we write the quadratic equation in the following form:
a{(x+m)^2} + n,
where m and n are constants.
Thus, we obtain a part expressed as (x+m). So, when we have this term squared, we have finally ‘completed the square’.
Completing the square calculator applications:
Completing the square method is useful in:
- Converting a quadratic expression into vertex form.
- Analyzing at which point the quadratic expression has minimum/maximum value.
- Graphing a quadratic function.
- Solving a quadratic equation.
- Deriving the quadratic formula.
Evidently, it is possible to use the complete square method for a variety of reasons. Nevertheless, its most common applications are the solving and the graphing of the quadratic solutions.
Complete the square steps
Step-1: Consider a quadratic equation in its standard form:
ax^{2}+bx+c=0,
Step-2: The coefficient of the term x^(2), has to be made 1.
Therefore, the value of ‘a’ has to be made 1.
To do this, we have to divide the quadratic equation throughout by ‘a’.
Thus, the equation now takes the form:
x^(2) + (b/a)*x+ (c/a) = 0.
Step-3: Shift the (c/a) term on the L.H.S., to the R.H.S.
Step-4: Multiply the coefficient of x, that is, the term (b/a) by 1/2.
Consider the result as ‘d’
Step-5: Square this value of ‘d’ and add the result to both the L.H.S. and the R.H.S.
Step-6: Consequently, the L.H.S. is expressed in the form of (x+d)^(2) and the R.H.S. gives us a
constant value.
Step-7: This is the final step. Calculate the square roots of both the L.H.S. and the R.H.S. Adjust the
sides and calculate for x.
As you can see, the value of x can be obtained in a very simple manner.
Completing the square calculator circle:
In general, any equation of the form Ax^2 + Ay^2 + Bx+ Cy + D=0 will produce a circle.
OUR GOAL: To find the standard form of the given circle equation by factoring.
In order to factor the original equation, we will need to add a “magic number” to BOTH sides of the equation. Remember, of course, that we can always add something to both sides of an equation without unbalancing it. In this case it will help us get the equation into a more useable form.
Example: Complete the square given the equation 4x^2 + 4y^2 − 24x + 32y – 4 = 0.
1) Do the squared terms have matching coefficients?
Yes. So, we have a circle here.
2) Can we make the squared terms have a coefficient of 1?
Yes, we can do this. How? By dividing EACH term in the equation by 4.
We now have an equation that looks like this: x^2 + y^2 − 6x + 8y – 1 = 0
3) Group the x terms and y terms together:
We rewrite our equation to get: x^2 − 6x+ y^2 + 8y − 1= 0
4) Complete the square for the x and y-terms SEPARATELY.
(x^2− 6x+ 3^2) + (y^2 + 8y + 4^2) − 1= 32 + 42
Basically, we took each of those X and Y sections and turned it into an easily factorable quadratic. By dividing the linear term coefficients (the 6 and the 8) by two and then squaring that, we found good numbers to add that make each section easily factorable. That’s where the 32 and 42 terms came from on each side of the equation.
5) Thanks to these magic numbers, we can now factor our equation.
Our equation becomes: (x−3)^2 + (y+4)^2 = 26.
Quadratic Equations:
In the context of algebra, there are several forms of equations. However, the Quadratic form of equations is one of the most common forms that you can face.
Quadratic equation standard form:
Any equation that can be rearranged in standard form as:
ax^{2}+bx+c=0,
wherex represents an unknown, and a, b, and c represent known numbers, where a ≠ 0, is known as a quadratic equation.
Explaining the above quadratic equation form,
Firstly, the quadratic coefficient is a,
Secondly, the linear coefficient is b and,
Finally, the constant or free term is c.
a, b and, c taken together are called the coefficients of the equation.
However, if the value of a=0, then the term a*x^(2) becomes zero. Hence, the equation no longer remains quadratic in nature and becomes linear.
For every quadratic equation, there can be one or more than one solutions. These are the roots of the quadratic equation.
Accordingly, for a quadratic equation ax^2+ bx + c = 0,
the sum of its roots = –b/a and the product of its roots = c/a.
Quadratic Equation basic concepts:
You can use various ways for solving quadratic equations. In total, there are four different methods to do the same:
- Factoring process,
- Using the square roots method,
- Completing the square method and,
- Using the quadratic formula.

However, in our article, we are mainly going to focus on the Completing the square method for solving quadratic equations.
Quadratic equations types:

Standard form:
Quadratic equations are generally expressed in standard form. However, not every quadratic equation you see will be in this form, it’s still helpful to see examples. Also, keep in mind that the quadratic coefficient ‘a’ cannot be a zero.
Examples of the standard form of a quadratic equation (ax² + bx + c = 0) include
- 6 x² + 13 x – 55 = 0
- x² – 3 x – 2 = 0
- -4 x² – x +12 = 0
- 20 x² -15 x – 10 = 0
- x² -2 x – 3 = 0
- 19 x² – 2 x – 9 = 0
- 3 x² + 8 x + 2 = 0
- -x² +7 x + 18 =0.
Missing linear coefficient:
Mostly, Quadratic equations look like this but the arrangement can also be different in some cases.
For example, there might be a few quadratic equations in which the linear coefficient ‘b’ is missing.
A few examples of this case are:
- x² – 64 = 0
- x² – 16 = 0
- 9x² + 49 = 0
- -2x² – 4 = 0.
In the above examples, the linear coefficient of the x term is missing.
Missing constant term:
Further, in a quadratic equation the constant term(c) might also be missing:
x² – 7x = 0
2x² + 8x = 0
-x² – 9x = 0
x² + 2x = 0
-6x² – 3x = 0
-5x² + x = 0.
Thus, the type of quadratic equations might not be the same at all times. You need to analyze any equation correctly and categorize it correctly.
Actually, this will help you to not make mistakes of confusing the values of a.b and, c.
Quadratic Equations roots formula:
Quadratic Equation by Factorization method:
Solving quadratic equations is nothing difficult. Apparently, you just need to follow a few rules and you are all set!
As mentioned earlier, the first approach you should try out is the ‘Factorization’ method.
We can obtain the two roots of the equation(p and q, say) via this process.
Finally, to solve the quadratic equation ax 2 + bx + c = 0 by factorization, perform the following steps:
- Firstly, expand the expression and clear all fractions if necessary.
- Secondly, move all terms to the left-hand side of the equal sign.
- Thirdly, factorize the equation by breaking down the middle term.
- Finally, equate each factor to zero and solve the linear equations.
Example 1:
Solve: 2(x 2 + 1) = 5x
Solution
Expand the equation and move all the terms to the left of the equal sign.
Or, 2x 2 – 5x + 2 = 0
Or, 2x 2 – 4x – x + 2 = 0
Or, 2x (x – 2) – 1(x – 2) = 0
Or, (x – 2) (2x – 1) = 0
Thus, equate each factor equal to zero and solve
⟹ x – 2 = 0 or 2x – 1 = 0
Or, x = 2 or x = 1/2.
Therefore, the solutions are x = 2, 1/2.
Example 2:
Solve the following quadratic equation (2x – 3)2 = 25.
Solution
Expand the equation (2x – 3)2 = 25 to get;
Or, 4x 2 – 12x + 9 – 25 = 0
Or, 4x 2 – 12x – 16 = 0
Then, divide each term by 4 to get;
Or, x 2 – 3x – 4 = 0
Or, (x – 4) (x + 1) = 0
Or, x = 4 or x = -1.
We hope this process has become clear to you now.
Finally, we are going to leave you a problem set for you to practice the ‘Factorization’ process.

Solve by ‘Completing the square’ formula:
Moving on, we have reached our main area of focus.
We have already discussed the steps that we need to follow to solve sums via the ‘completing the square’ method.
So, let us now discuss some examples:
Example 1:
Solving x2 – 6x – 3= 0 by using completing square method formula –
x2 – 6x – 3 = 0
Or, x2 – 6x = 3
Or, x2−6x+(−3)2 = 3+9
Or, (x−3)2 = 12
Or, x−3 = ± √12 = ±2 √3
Or, x = 3±2√3.
Example 2:
4x2 + 12x + 1= 0
Or, x2 + 3x = – (1/4)
Or, x2 +3x + (3/2)2 = -(1/4 ) + (3/2)2
Or, (x +3/2)2 = 8/4
Or, (x + 3/2) = 2√2 / 2 = √2
Or, x = √2 – (3/2).
Given below is a set for you to solve using the Complete Square Method:

Quadratic Equation use in real life:
Quadratic equations can form a very important part of cost-analysis problems or a few decision-making problems as well.
So, knowing the ‘completing the square’ method for solving them also becomes quite crucial.
Read Also: Parabola Calculator- parabola equation, meaning, formula
Here, we will provide you with some examples to prove how quadratic equations are an important part of some decision-making scenarios.
Example 1- Calculating areas:
Suppose, you need to find the area of a hall, a garden or a room. In fact, let the problem be such that there exists a rectangular room that has a length that is three times its breadth. On the other hand, you just have 7 square feet of wood to cover its ground. If you arrange this in the form of an equation, then it will take on a quadratic form.
Obviously, the value of the area (3*x*x) must be less than or equal to 7. Fulfilling these conditions satisfy the constraints. Solving this equation, we can find the value of x.

Example 2- Business decision making:
Let’s say that you are an operating firm. Consequently, figuring your firm’s profits is an important task for you.You need to know the number of units of goods that you have to sell in order to generate a profit, right?
As you can see, a basic knowledge of quadratic equations and the ‘completing the square’ method will come in really handy in such situations.
The price of the good is the factor on which the product demand is most likely to depend. So, let us keep it a variable ‘p’. Suppose, you want to sell 18 units of the product. The demand function your firm faces is (18-p). So the revenue would be p times the demand, that is, {p*(18-p)}. Further, if you equate your firm’s obtained revenue to the production costs you face, then you will reach the break-even point. It simply results in a good old-fashioned quadratic equation once again. Thus, you can calculate the price(p) that you need to set at this level.
The two examples mentioned above are one of the few instances of the importance of quadratic equations.
In conclusion, quadratic equations are of great significance in the context of algebra. So, it is obviously important for us to master the methods of solving them. The ‘Completing the square’ method is quite simple and you can use it in most cases.
Completing the square method FAQs:
What is the purpose of ‘Completing the square’?
The ‘Completing the square method’ is used to solve a quadratic equation and find its roots, namely ‘alpha’ and ‘beta’. In this method, the form of the quadratic equation is changed in such a way that the left hand side of the equation becomes a perfect square trinomial.
Does completing the square method always work?
Yes, indeed. This method always works. It is unlike the factorization process which requires the Trinomial be factorable.
Who is the Father of the Completing the Square method ?
MuhammedIbn Musa Al-Khwarizmi is regarded as the father of the ‘Completing the Square’ method. It is a very significant method of solving quadratic equations.
Is Completing the square method the only way to solve Quadratic equations?
No, that is definitely not true. Apart from using the complete square method to solve quadratic equations, you can also use the Factorization process, the square root method or even the quadratic formula, for that matter.
Is the completing the square calculator easy to use?
The ‘Completing the square’ calculator is very easy to use since we do not need to memorize any formula for using it. Simply, plug in the values of the coefficients (a and b) and the constant (c) in the available boxes. Accordingly, the result is displayed after clicking on the ‘calculate’ button.
Why is ‘Completing the square’ method better?
We generally apply the ‘Completing the square’ method on quadratic equations that are not factorizable. Via this process, we basically turn the Left hand side of the equation into a perfect square trinomial. In other words, it is simply a method to transform a non-factorizable equation into a factorizable one.
The form of the equation, thus becomes (x + m) ^ 2 = constant.
When will ‘Completing the square’ method not work?
The ‘completing the square’ method will not work if the quadratic coefficient(a) is not equal to 1. In order to ensure this happens, if ‘a’ is not equal to 1 in a given quadratic equation, then simply divide the equation throughout by ‘a’. This will cause the quadratic coefficient to become one.
Does the ‘Completing the square’ have any other applications?
Yes, the ‘completing the square’ method is very useful in other cases as well. It definitely provides an alternative for factorizing a quadratic equation in order to solve it.
However, it is useful for writing equations in specific formats as well.
For example, the standard form of a circle is written as:
(x – h) ^ 2 + (y – k) ^ 2 = (r) ^ 2.
Also, the vertex form of a quadratic equation (a parabola) is written as:
G( x ) = a * (x – h) ^ 2 + k.




