A distributive property calculator is a different type of calculator that displays the solutions to some mathematical problem. This type of calculator calculates problems using the distributive property. The distributive property is a multiplication calculator used for addition and subtraction. The distributive property is also known as the distribution law of multiplication and division. This type of calculator is faster than normal calculators. It saves your time also.
So, keep reading to know about this distributive property calculator.
Distributive property calculator with steps
A distributive property calculator is an online calculator. So, it is very easy to use. There are only three steps to do the solution. These steps are:
- First, in the input field, type an expression of the form a (b+c).
- Then, to obtain the simplified phrase, click the “Submit” button.
- Finally, what will present the simplified version of the specified statement in a new window.
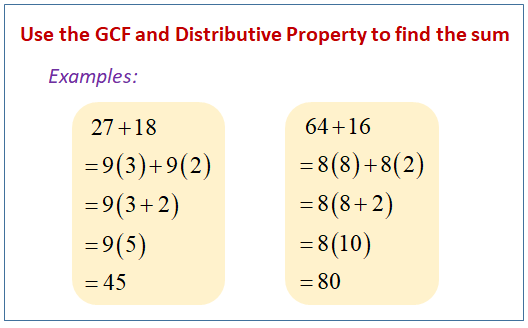
Numbers in mathematics should obey the characteristic feature during arithmetic operations. Associative property, commutative property, distributive property, inverse property, identity property, and so on are examples of properties. The distributive property allows us to multiply a number by a set of added numbers. a(b+c) = ab + ac is the distributive property.
Distributive property calculator with variables
We can solve any variable-containing equation by using the distributive principle with variables. As an example, 123456 × 654321=? So, this is the equation that we will solve now.
Now we just put the equation in our distributive property calculator. Then, click the submit button, and a new window will open. Finally, we will get the answer.
If we don’t use the property calculator, we can solve it with a normal calculator in big steps. So, at first, we write the first number (123456). Then, we will use the distributive law to break up the number 654321. So, we need to write 65 and then multiply by ten thousand. Then, we will add plus 4521 and apply the distributive law. So, now we get 123456 and then multiply it by sixty-five.
Then, we will add on the zeros again from the ten thousand plus 123456 multiplied by 4321. Now, let’s get our calculator and try to deal with these. So, 123456 multiplied by 65 gives us 8024640. We will still have to multiply by ten thousand. In the other piece, 123456 multiplied by 4321 is 533453376. So, we have 80246400000 plus 233453376. So, the answer is 80779853376.
Distributive property calculator fractions
Involving fractions in any phrase enhances its complexity. So, there is a way to reduce this complexity to keep the distributive property remaining the same. So, the general form of distributive property is:
- a/b*(c+d) = a/b*c + a/b*d (Left distributive property)
- (a+b)*c/d = a*c/d +b*c/d (Right distributive property)
We can easily calculate this type of equation using the distributive property calculator.

Distributive property examples
1. 3 times (12 plus 5)
2. If you look at the first one there, it says three times the sum of 12 and 5 or the sum of 12 plus 5. So, the distributive property takes the number that’s on the outside of the parentheses. Then, we will multiply it by every number that’s on the inside of the parentheses. So, how we like to remember that is “Say hi multiply.” So, what that means is I like to think of parenthesis as a house, and inside the house is a 12 and a 5. Now, 3 is outside the house, and he is trying to get inside the house. And in order to do so, he needs to “say hi” to each of the numbers inside by multiplying. So, the first three will multiply with 12, and then he is going to multiply with 5. Next, put the plus between these two equations. So the answer is 51.
3. 6 times (4 minus 3)
4. So, for this equation, how we like to remember that is “say bye multiply.” Five is outside the parentheses, so five needs to say bye to the 4. Then, it will be four multiply six and also needs to “say bye” to the 3. So, it’s going to also be six times 3. Next, put the minus between these two equations. So, the answer is 6.

Other examples
| 5 (x-2) = 100 | We have a set of parentheses with 2 terms inside. |
| 5x – 10 = 100 | Distribute: 5(x) – 5(2) |
| 5x – 10 + 10 = 100 + 10 | Add 10 both sides. |
| 5x= 110 | Now, we have a one step equation. |
| 5x/5 = 110/5 | Divided by 5 both sides. |
| x= 22 | Solution of 22. |
| 5 (x-2) = 100
5 (22-2) = 100 100 = 100 |
Proved. |
Next,
| 2x – 3 (2x – 3) + 4 = 33 | We have a set of parentheses with 2 terms inside. |
| 2x – 6x +9 + 4 =33 | Distribute: -3 (2x) = -6x -3 (-3) = 9 |
| -4x + 13 = 33 | Combine them. |
| -4x +13 – 13 = 33 – 13 | Subtract 13 from both sides. |
| -4x = 20 | Now, we have a one step equation. |
| -4x/-4 = 20/-4 | Divided by -4 both sides. |
| x= -5 | Solution of -5. |
Distributive property of multiplication over addition
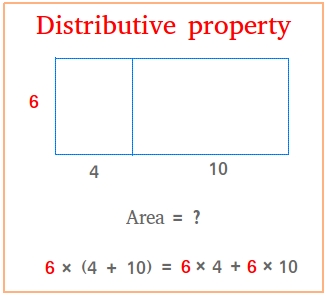
Distributive property, as the name suggests, a number or a multiply can be distributed among the two addends. According to the distributed property of multiplication, if there are three numbers: A (B + C), so A (outside the bracket) is distributed among the two inside numbers. So, we are just multiplying the outside number with the two inside numbers. Then, we are going to add the numbers. Hence, it is called the distributive property of multiplication over addition. So, we are not going to add two numbers first. We multiply the numbers then add the two numbers. So, clarify this with examples: 2(5 + 2).
So, according to the distributive property of multiplication, this will be:
2(5) + 2(2), which is 10 plus 4, which gives us 14.
Now let’s see if we are not using the distributive property and just adding the two numbers first. We get two times seven which is 14. So, the answers are the same.
Some frequently asked questions
What is a distributive property in math?
A distributive property calculator is a different type of calculator that displays the solutions to some type of mathematical problem. This type of calculator calculates problems using the distributive property. The distributive property is a multiplication calculator that can be used for addition and subtraction. The distributive property is also known as the distribution law of multiplication and division.
What is a distributive property with an example?
Three times (12 plus 5)
- If you look at the first one there, it says three times the sum of 12 and 5 or the sum of 12 plus 5. So, the distributive property takes the number that’s on the outside of the parentheses. Then, we are going to multiply it by every number that’s on the inside of the parentheses. So, how we like to remember that is “Say hi multiply.” So, what that means is I like to think of parenthesis as a house, and inside the house is a 12 and a 5. Now, 3 is outside the house, and he is trying to get inside of the house. And in order to do so, he needs to “say hi” to each of the numbers inside by multiplying. So, the first three are going to multiply with 12, and then he is going to multiply with 5. Next, put the plus between these two equations. So the answer is 51.
What does the distributive property look like?
Numbers in mathematics should obey the characteristic feature during arithmetic operations. Associative property, commutative property, distributive property, inverse property, identity property, and so on are examples of properties. The distributive property allows us to multiply a number by a set of added numbers. a(b+c) = ab + ac is the distributive property.
What is an example of the associative property of multiplication?
According to the associative feature of multiplication, the product of three or more integers remains constant regardless of how the numbers are arranged. For instance, three into (5 into 6) Equals (3 into 5) into 6.
How do you do distributive property on a calculator?
A distributive property calculator is an online calculator. So, it is very easy to use. There are only three steps to do the solution. These steps are:
- First, in the input field, type an expression of the form a (b+c).
- Then, to obtain the simplified phrase, click the “Submit” button.
- Finally, What will present the simplified version of the specified statement in a new window.
How do you use the distributive property to write an expression without parentheses?
You may simplify things by expressing an equivalent phrase without the parenthesis. First, multiply five by each of the terms included in parenthesis. Next, simplify each portion of the phrase before adding them together. 5(2+3)=25 is the answer.
What is the area formula?
Area = w × h is the area formula where w = width, h = height.




