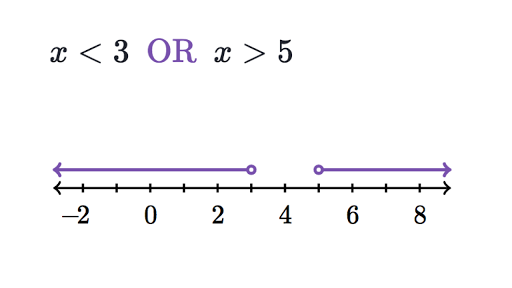‘Compound Inequality Calculator’ – sounds complicated, right?
It might be a cakewalk for maths geeks but wait, let this article be your savior.
Let us dive into the topic and find out what it is all about. Let’s understand it from the point of view of a 10-year-old.
WHAT IS A COMPOUND INEQUALITY CALCULATOR?
Compound Inequality Calculator is a tool that will help us to calculate problems on compound inequality instantly.
Click here to access the calculator.
STEPS TO USE THE COMPOUND INEQUALITY CALCULATOR
Follow the steps to solve a compound inequality using the calculator :
The procedure to use the compound inequality calculator is as follows:
Step 1: Enter two inequality equations in the respective boxes
Step 2: Choose the </>/≤/≥ signs as per the problem for respective equations.
Step 3: Choose AND/OR from the drop-down menu
Step 4: Click the SOLVE button
Finally, the Compound Inequality Calculator will generate the results in a new window.
The result will show the solved inequality along with the number line.
Now, let us understand the whole concept of Compound Inequality.
COMPOUND INEQUALITY CALCULATOR NUMBER LINE
The calculator tool automatically plots a number line of the compound inequality fed to it. The number line shows the extent of the solution set.
Let’s learn how to graph a number line manually.
COMPOUND INEQUALITY CALCULATOR GRAPH
We are going to represent x: 3 x + 2 < 14 and 2 x – 5 > –11 on the number line.
Let’s solve it first.
The following picture shows its solution. Refer to the inequalities problem we solved above, you will get the hang of it.

x < 4 indicates all the numbers less than 4, and x > –3 indicates all the numbers greater than –3. The intersection of these two graphs of the inequalities is all the numbers between –3 and 4.
The solution can be also represented in the form of a solution set as follows:
{ x| x > –3 and x < 4}
The Compound Inequality will be represented as follows on the number line:
![]()
In the picture above, the grey shaded line shows the values of x ranging from -3 to 4.
The points -3 and 4 on the number line have an empty dot over them implying the exclusion of the respective numbers.
Empty dots are used when < or > is used in inequalities.
In contrast, the number line for the solution set of –9 ≤ x and x ≤ 1 will be as follows:
![]()
The grey shaded line shows the values of x ranging from -9 to 1. Note how the dots over points -9 and 1 are colored. The colored dots simply imply the inclusion of the respective numbers i.e. in this case it is -9 and 1.
Colored dots are used when ≤ or ≥ are used in inequalities.
COMPOUND INEQUALITY CALCULATOR INTERVAL NOTATION
Compound Inequalities can also be presented in the form of an Interval Notation.
The solution fetched from the calculator can be represented in the form of an interval notation manually.
Interval notation is a way to represent the solution set of a solved compound inequality. It is represented using a round bracket ‘(‘ / ‘)’ or square bracket ‘[‘ / ‘]’
For example, if a solution set is −4 < x < 3
The interval notation would be ( -4, 3 ) , the smaller number written first
Explanation: Round bracket or ‘(‘ / ‘)’ is used since ‘<’ appear in the solution set. Round bracket means exclusion of the points.
Let’s take another example: -2≤x≤1
The interval notation would be [-2,1] , the smaller number written first
Explanation: Square bracket or ‘[‘ / ‘]’ is used since ‘≤’ appear in the solution set. Square bracket means inclusion of the points.
INEQUALITY DEFINITION
Firstly, let us understand the meaning of ‘Inequality’ in the context of Mathematics.
An inequality compares two values, showing if one is less than, greater than, or not equal to another value. An inequality shows the relationship between two values in an algebraic expression that are not equal. When we are performing algebraic operations on inequalities, it is important to conduct accurately the same operation on both sides to preserve the truth of the statement.
INEQUALITY EXAMPLES
Inequalities have the following forms:
x ≠ y means that x is not equal to y
x < y means that x is less than y
x > y means that x is greater than y
x ≤ y means that x is less than or equal to y
x ≥ y means that y is greater than or equal to y.
Now, let’s understand what is Compound Inequality?
COMPOUND INEQUALITY DEFINITION
A compound inequality comprises two or more inequalities joined together with OR or AND. If the inequalities are connected using the word AND, it implies that the inequalities are true at the same time. If the inequalities are connected using OR, it implies that at least one of the inequalities is true.
COMPOUND INEQUALITIES ‘AND’ VS ‘OR’
A compound inequality is made up of at least two inequalities that are separated by either “and” or “or”.
COMPOUND INEQUALITY CALCULATOR ‘AND’ COMPOUND INEQUALITIES
The solution of a compound inequality comprises two inequalities connected with the word and is the intersection of the solutions of each inequality. Both statements must be true at the same time. The solution to an and compound inequality ishas all the solutions that the two inequalities have in common. The graphs of these two inequalities will overlap on plotting. The solution set of the “and” compound inequality is the intersection, represented by the INTERSECTION symbol ∩, of the two inequalities.
Let us take an example:
2 + x < 5 and -1 < 2 + x
We will deal with the two inequalities separately.
Firstly,
2 + x < 5
To eliminate the variable, we will subtract 2 from both sides.
2 + x – 2 < 5 – 2
or x < 3
For the second inequality,
-1 < 2 + x
We will subtract 2 from both the sides
-1 – 2 < 2 -2 + x
or -3 < x
Therefore, the solution for this compound inequality is x < 3 and -3 < x, or -3 < x < 3.
-3 < x < 3 , this implies that the value of x lies between -3 and 3.
COMPOUND INEQUALITY CALCULATOR ‘OR’ COMPOUND INEQUALITIES
The solution of a compound inequality that comprises two inequalities connected with the word or is the union of the solutions of each inequality. Unions allow us to create a new set from two that may or may not have similar elements. It involves solving two linear inequalities joined by the word “or”. On solving we get a solution that works on at least one inequality. The solution set of the “or” compound inequality is the union, represented by the UNION symbol ∪, of the two inequalities.
Let’s take an example:
7 > 2x + 5 or 7 < 5x – 3
We will deal with each inequality separately.
For 7 > 2x + 5, we subtract both sides by 5 to get
7 – 5 > 2x + 5 – 5
or 2 > 2x
Now, dividing both sides by 2, we get
1 > x
For 7 < 5x – 3, add 3 to both the sides
7 + 3 < 5x – 3 + 3
or 10 < 5x
Dividing both sides by 5, we get
2 < x
Hence, the solution for this compound inequality is x < 1 or x > 2
There will be two solution sets in this case.
One has values of x which are less than 1.
The other has values of x which are greater than 2.
DOUBLE INEQUALITY DEFINITION
Double Inequality takes the form of a<x<b. When solving a compound inequality in the form of a<x<b, the easiest approach is to break the compound inequality into two separate inequalities, that is, x<b and x>a. After solving the two inequalities separately, we can combine their results using and to find the solution to the compound inequality.
Let’s have a better understanding with an example:
3+x>7x−2>5x−10
We will solve 3+x>7x−2 first.
Subtracting x from both the sides
3 + x – x > 7x – x – 2
or 3 > 6x – 2
Adding 2 to both sides
3 + 2 > 6x – 2 + 2
or 5 > 6x
Dividing 6 from both sides, we get
⅚ > x
Now, we will solve 7x−2>5x−10
Subtracting 5x from both the sides,
7x – 5x – 2 > 5x – 5x – 10
or 2x – 2 > – 10
Adding 2 to both the sides,
2x – 2 + 2 > -10 + 2
or 2x > -8
Dividing both the sides by 2, we get
X > -4
Hence, we have two solutions, ⅚ > x and X > -4
The solution set is −4 < x < 5/6
The solution set can be also represented in the form of an interval notation.
The interval notation, in this case, will be ( -4, ⅚ ), the smaller number will come first.
Congratulations! You have successfully understood the basic idea of compound inequality. (Hope so 🙂 )
Time to level up a bit. Let’s continue with the ride.
CONJUNCTION AND DISJUNCTION IN COMPOUND INEQUALITY
We have already covered the concept of conjunction and disjunction in the parts above. Let’s get familiar with the terminology.
A compound inequality where the two inequalities are separated using the word “and” is called a conjunction. Although in the English Language “and” and “or” are parts of speech known as conjunctions, the mathematical conjunction has a distinct meaning.
The conjunction (in English Grammar) “or”—when used in a compound inequality— is called a disjunction.
3 x + 4 < 14 and 2 x – 7 > –11, this is a conjunction
2 x + 8 < –11 or –3 x – 2 < 15, this is a disjunction
COMPOUND INEQUALITY IN THE REAL WORLD
No, such complex maths is not just limited to textbooks. It has various applications in our daily life.
- TIER SYSTEM: A tier system is a method of organizing data into separate categories, called “tiers.” Data is placed in each category based on certain criteria, which, for example, can be students’ marks, or an individual’s income. The tier ranking system is built on conjunctions: Each tier contains entries better than that of the lower tier and worse than entries of the tier above. The result is a chain of inequalities, such as Tier 1 > Tier 2 > Tier 3 and so forth.
- DETERMINING SECTIONS: Compound inequalities allow to demonstrate the extent of regions, layers, or stages. For example, the Stratosphere, the second layer of the Earth’s atmosphere, is not less than 10 miles and at most 31 miles over the surface of Earth. If “x” is the stratosphere, we can write down this compound inequality as 10<x<31.
- DESCRIBING EXTREME VALUES: Disjunctions are used in real life to illustrate extreme values on either side of a theoretical axis. An example of such an axis can be that of age. For example, the non-working age group of people ranges from ages 18 to 65. Therefore, the compound inequality would be x<18 or x>65. Similarly, severe weather conditions occur when the temperature is above 40 or below 1 degree Celsius, which you write as x<1 or x>40.
- APPROXIMATIONS: Approximations can be represented as conjunction if it is sure that the exact number cannot be more or less than certain values. For example, you may know the exact salary of a person, but you are sure it’s not more than Rs 15,000 and not less than Rs 5000. Therefore, her salary is Rs 5000<x<Rs 15000. Similarly, when you try to determine the age of a person, you may say he is more than 30, but not more than 40, which you can express as 30<x<40.
CONJUNCTION EXAMPLE
An example of a compound inequality involving the word “and” can be that of an elevator. An elevator for a building must be greater than (or equal to) floor zero and the top floor. For a 30-floor building, the elevator reaches all the floors between the ground floor and the top floor, or 0≤x≤30. In other words, we can say that the elevators should be able to reach greater than or equal to the ground floor AND less than or equal to the 30th floor.
DISJUNCTION EXAMPLE
An example of a compound inequality involving the word “or” can be thought of as a car burning fuel. A car burns more petrol when it is going either slow or very rapidly. For instance, a car going below 35 miles an hour or higher than 75 miles an hour uses more fuel. As a result, it is very costly. The inequality equation to display this is the speed is less than 35 miles per hour OR greater than 75 miles per hour. Similarly, we can say, x<34 or x>75.
We have had an in-depth understanding of the concept of Compound Inequality.
This brings us to the end of the article. We have had an overview and understanding of the fundamentals and applications of Compound Inequality. Hoping that after reading it you will have a good understanding of the topic. Also, help those who struggle to understand it.
The Compound Inequality Calculator is a cherry on the cake!
Try solving compound inequalities problems yourself first before taking the help of the calculator!
COMPOUND INEQUALITY CALCULATOR SYMBOLAB
Symbolab is a very popular compound inequality calculator. And not only compound inequalities, you can also calculate inequalities like linear, absolute value and system inequalities. Moreover the Symbolab inequality calculator is completely free of cost. You just need to enter your equation in the provided space. In addition, you will also find symbols which you can use to properly enter your equation.
FAQ
How do you solve the compound inequality?
First, separate the compound inequality into two inequalities. Solve the inequalities one by one.
What is the difference between and/or in inequalities?
When ‘and’ is used in a compound inequality, the solution would satisfy both the inequalities.
When ‘or’ is used in a compound inequality, the solution would satisfy either of the inequalities.
What is interval notation in inequality?
Interval notation is a way to represent the range of values that makes an inequality true.
What do ≠, <, >, ≤, ≥ mean?
x ≠ y means that x is not equal to y
x < y means that x is less than y
x > y means that x is greater than y
x ≤ y means that x is less than or equal to y
x ≥ y means that y is greater than or equal to y.
What is the union of two inequalities?
It is the intersection of the solutions of each inequality.
Which inequalities have no solution?
Inequalities that result into a false statement have no real solutions.